
Notice the inside function does not change when you derive the outside function. The chain rule say that if you have an "inside function" and an "outside function," then you take the derivative of the outside function, and multiply that by the derivative of the inside function, or So if we're looking at #y=arctan(cos(x))#, then we apply the derivative rule above, with the chain rule. Then by the Pythagorean Theorem, the hypotenuse can be found: Than means that there is a right triangle somewhere where the angle is y and the tangent of that angle is x, or #x/1#. Not in the first year of Calculus, anyway. We don't usually have derivatives that still have y's in them. We just derive everything as we go along, and we write #dy/dx# after every term that contains a y (that's a very, very over-simplified explanation of implicit differentiation, but it will work for this problem).

That's where we don't care whether or not we're looking at a function, that is, we don't care if we have y on one side and everything else on the other. Notice the tangent is no longer an inverse after the switch. So #y=tan^(-1)(x)# means the same thing as To invert means to switch the x and the y (among other things, but that's the important meaning here). If we were looking at #y=arctan(x)#, there's a way to determine the derivative if you've forgotten the formula.įirst remember that #arctan(x)# means "inverse tangent of x," sometimes written as #tan^(-1)(x)#.
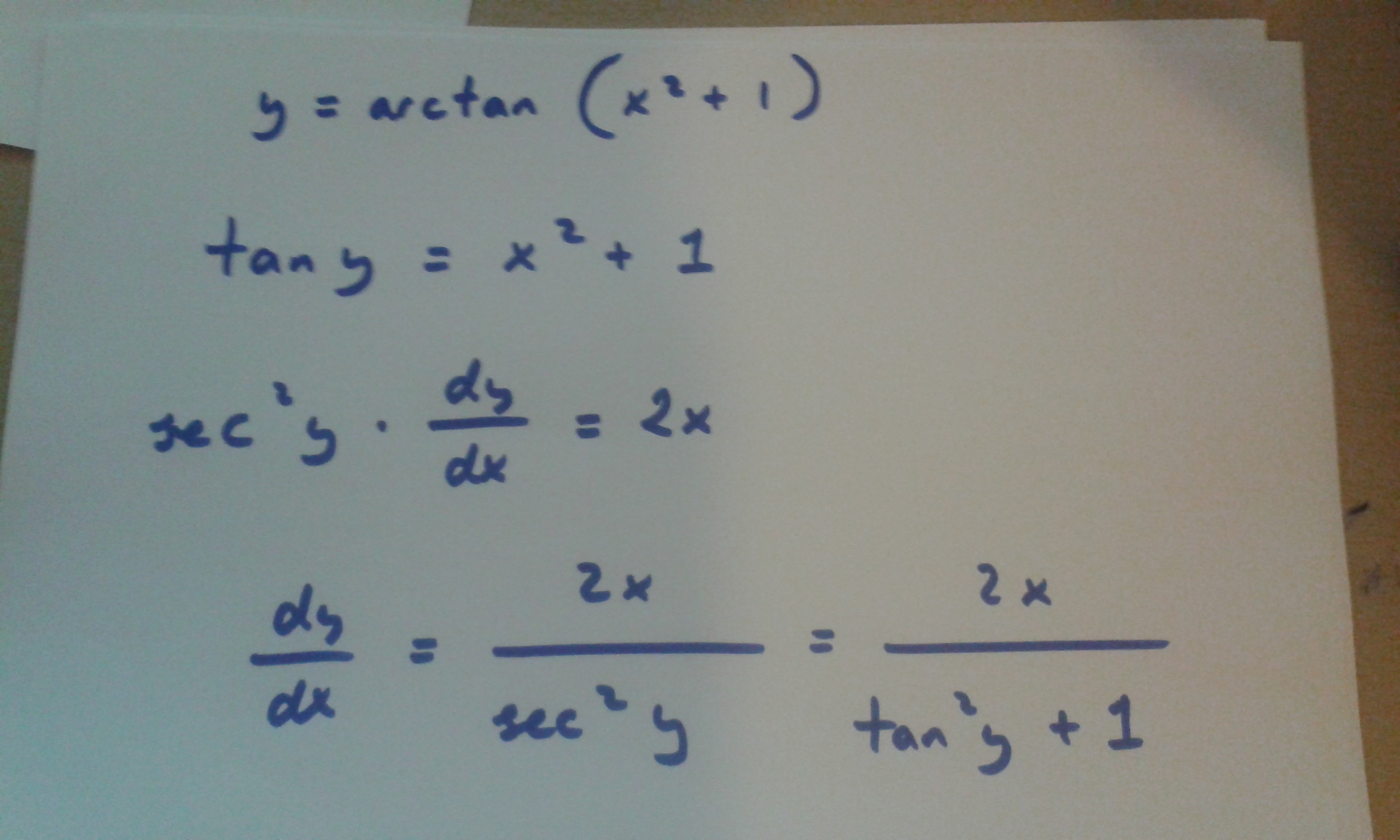
This is a case of knowing the how the derivative of inverse tangent works, and then following the chain rule.


 0 kommentar(er)
0 kommentar(er)
